Welcome to the Makse lab

Top cited articles

Research Projects

• 

  Predictions

  Using machine learning and statistical physics to predict human behavior

  Predictions

  ---

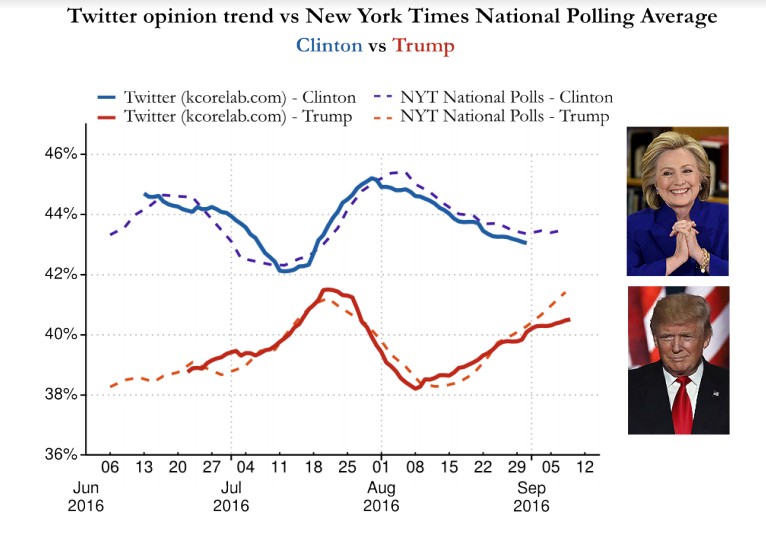
  Volume 355 of Science (February 03, 2017) focuses on the use of scientific methods to predict population-level trends. The work of Alexandre Bovet, Flaviano Morone, and Hernán A. Makse using analysis of Twitter to predict the outcome of the 2016 US Presidential Election is featured in John Bohannon’s article The Pulse of the People. Technology and understanding of human motivations and current circumstances are key to this type of prediction. Although there is still work to be done before a completely accurate method of prediction is attained, the tools we are developing at present are a step firmly in the right direction.

  A study by Bovet, Morone, and Makse (2016, paper here) has offered new insight into the use of social media to predict population-level trends in real time. Our results show that the holy grail of social media has been realized: our media analytics can replace the whole of the 19-billion-dollar-revenue polling industry with a free Twitter machine learning algorithm.

  As a case study, Bovet, Morone, and Makse found that it was possible to faithfully predict (r = 0.9)  by 6 to 15 days the aggregated polls on the front page of the New York Times website during the election, using only Twitter posts related to the 2016 Presidential Election. A network was constructed from interactions (mentions, tags, and re-tweets) among 73 million Twitter posts collected during the three months from the 1st of June to the 1st of September 2016, and natural language processing was used to infer the opinion of the post about a given candidate.

  Using percolation theory, several components of this network were identified: strongly- and weakly-connected giant components, and a corona of nodes that belonged to neither of these. Analysis of this network found that the strongly-connected giant component skewed more pro-Trump (possibly signifying the enthusiasm he had built among his supporter base) while Hillary Clinton was the most popular candidate if the entire network was taken into account. Further analysis immediately prior to the election predicted a very close win for Hillary Clinton, who indeed won the popular vote by close to 3 million votes.

  Through the methods pioneered in this study, which combine machine learning and tools of statistical physical analysis, and related ongoing work in the group, it is shown that analysis of a network of social media posts can forecast trends on the level of the national population. This is not only a valuable tool for sociological analysis, but has wider implications for marketing brands and products. Our methods accomplish what many firms charge considerable sums of money to do, at a fraction of the cost.

  Further information can also be found at the Kcore Lab website.

  Prediction and its limits, Science article (2017, vol. 355) by Barbara R. Jasny and Richard Stone

  The Pulse of the People, Science article (2017, vol. 355) by John Bohannon

  Further press releases are aggregated here.

     

  Other recent work involves the inference of financial status from telecommunications data. In a study to be published in Nature Communications, we combine machine learning methods and complex network analysis to infer individuals’ socioeconomic standings based on a nationwide mobile communications network and associated credit limit data. We find that the wealthiest 10% of the population tends to have the most diverse and intense communication patterns as compared to middle-class and poor individuals, i.e., they are the network’s “hubs” and are strongly-connected to other hubs, while those who are less affluent tend to only be weakly-connected to hubs. Moreover, we find via a targeted marketing campaign that a Collective Influence (CI) algorithm is the most effective predictor of financial status. The results of this study have wide-ranging applications to increase the efficiency of targeted financial endeavors, from marketing to economic stimulus.

  

  “Three Worlds”: A geolocation based visualization of a nation-wide mobile network. Three layers separate the groups with different socioeconomic status: the wealthy (top 10% total credit limit), the middle class (50~60% percentile) and the poor (bottom 10%). Those with top socioeconomic status are likely to have more intense and diverse communication patterns than other groups.

  S. Luo, F. Morone, C. Sarraute, M. Travizano, H.A. Makse. Inferring personal financial status from social network location, Nat. Comm., to appear (2017).

• 

  Brain Networks

  Theory of Optimal Influence in the Brain

  Brain Networks

  ---

  Background Theory

  The theory of optimal percolation is currently being applied to understand the structure of the brain following our recent studies in Morone, Makse, Nature (Aug 2015). We have developed the analytical solution to the problem of identifying of the most influential nodes (essential nodes) in complex networks [3]; a long-standing problem in data science [8]. This problem belongs to the class of non-deterministic polynomial-time hard problems (NP-hard), and therefore it is analogous to the hardest problems in computational science and spin glasses.

  

  Fig. 1: In brain networks, some nodes are more important than others. Morone and Makse, Nature 2015 [3]. The most important nodes are those whose elimination induces the network’s collapse, and identifying them is crucial in many circumstances, for example, to understand critical areas in the brain. But this is a hard task, and most methods available for the purpose are essentially based on trial-and-error. Morone and I have devised a rigorous method to determine the most influential nodes in net-works. We find that low-degree nodes surrounded by hubs as shown here play a much more important role in the network than previously thought.

  Our group has developed a large-scale search engine for localizing the most influential nodes in networks: the Collective Influence (CI) theory. CI combines optimality, scalability and versatility, making it applicable to a large class of problems, e.g., from finding influential areas in the brain, to containing epidemic outbreaks through targeted immunizations, maximizing the spreading of information in social media, or quantifying systemic risk in banking systems. We show that tools of combinatorial optimization, spectral theory, spin glasses and machine learning can be used to find the essential nodes in the network. The theory provides a ranking of nodes whose inhibition produces the largest disrupting cascading effect extending to a large portion of the brain. Applying the theory of collective influence in the brain is the focus of our current and future research program as discussed next.

  The data that we used in this study can be downloaded here.

  Theory of Collective Influence in the Brain

  Accumulating evidence suggests that alterations in the functional brain network may lie behind a number of neurological and neuropsychiatric conditions. Existing interventional techniques (e.g. deep brain stimulation, transcranial magnetic stimulation) are currently being applied without taking into account the alterations in network dynamics thought to be at the root of neurological maladies. Our main hypothesis is that a therapeutic window exist to control network dynamics with targeted interventions to essential node’s activity rigorously predicted by our network theory of Collective Influence in the brain. The rationale is that the activation/deactivation patterns applied to the essential influential nodes predicted by our graph optimization theory will propagate through the central nervous system to impact and modulate brain network dynamics. Our theoretical advances allows researchers and treating clinicians to accurately identify new targets for focal therapy and to move away from “trial and error” therapeutic approach often currently employed. Our theories will allow neuroradiologists, neurosurgeons and the broad neuroscience community to identify and analyze the most influential parts of the brain in various disease states. The tools developed by us will aid in the understanding, diagnosis, and therapy of brain disorders thought to be due to disruptions of brain connectivity (e.g. brain tumors, Alzheimer’s disease, ADHD, strokes or traumatic brain injury). To this end, we are following two complementary research programs in rodents and humans that are providing the scaffold to test our hypotheses.

  A. Manipulating essential nodes for integration in a in-vivo animal model of learning and memory guided by network optimization theory (NSF-CRCNS)

  Our goal is to identify and manipulate nodes in the brain that are essential for global integration of information. This is crucial for a fundamental understanding of how the brain works as well as to treat neurological and psychiatric conditions. Evidence suggests that a few essential nodes in the brain control a number of crucial functions, such as memory formation, conscious perception and attention, as well as critically participating in brain dysfunctions. However, finding and manipulating essential nodes to control brain network dynamics has not been possible due to the lack of a theoretical framework that could guide prospective interventions.

  Selection of targets and stimulation protocols in most studies are based on a questionable trial-and-error approach. What is fundamentally lacking is a network theory to guide these interventions. Advanced network theory applied to the brain will allow researchers and clinicians to prescribe targeted interventions to critical brain nodes.

  Our Collective Influence network optimization theory [3, 2] allows to accurately predict the effect of targeted inactivation of essential nodes in the network. Specifically, we use optimal percolation theory to identify the most influential nodes in a system-wide brain network formed in an in-vivo animal model of learning and memory (Fig. 2). Our network optimization theory predicts that the nucleus accumbens (NAc), a well-known structure in the meso-cortico-limbic system, is the most influential node for the interaction between the hippocampus (HC) and the prefrontal cortex (PFC) and the formation of an integrated memory network. This prediction is confirmed by the inhibition of a single core node in the NAc, using a targeted pharmacogenetic intervention, which remarkably, completely eliminates the formation of the memory (Fig. 3) [1].

  

  Fig. 2: Collective Influence theory [3] predicts the es-sential nodes in a memory network induced by LTP in rats. a, Relative size of the giant connected component G of the memory network formed by HC, PFC and NAc under LTP as a function of the fraction of inactivated nodes, q. Shown are two strategies for choosing the essential nodes: Hub-inactivation (triangles) and CI-inactivation (circles). Most of the hubs (red symbols) are located in HC, yet, they are not essential for integra-tion: the hub-inactivation curve shows minimal damage to G upon removal of hubs. On the contrary, by just inactivating 7% of high CI nodes, the giant component collapses to almost zero. This in-dicates that the high CI nodes are the essential nodes in the NoN. Most of the essential nodes are in the NAc as seen by the major-ity of green symbols along the curve. b, Representative NoN for the same system as in a, displaying the PFC-HC-NAc networks. The size of nodes is proportional to CI. Most of the high CI nodes are in the NAc. c, We inactivate the top 3% of high CI nodes (yellow circles) and G is drastically reduced to less than 40% of its original value. These top CI nodes are all in NAc except for two nodes in PFC. d, Further inactivating upto 7% of the high CI nodes completely prevents integration of G. Yellow circles indicate the essential nodes which are in their majority located in NAc. e, Average CI map indicating how many times every node appears as a top CI node over six animals. Color bar represents the average CI rank. White areas correspond to the top essential nodes for integration which are all located in the NAc.

  In our experiments the nucleus accumbens (NAc) is identified as the essential node in the memory network–a finding that had not been anticipated by conventional hub-centric theory. Importantly, this empirical finding alters the prevailing view of the role of the NAc in memory formation. Previously the NAc had been seen as down-stream of the hippocampus and prefrontal cortex. Our data ascribes to the NAc an important up-stream modulatory role in memory formation.

  

  Fig. 3: Experimental confirmation in the memory model [1]. a, The inhibitory version of DREADD receptors (hM4Di) is expressed in the NAc using a combination of two adenoassociated viruses (AAVs) injected stereotaxically in the nucleus as indicated. b, Histological verification 4 weeks after the viral infection. c, d, and e, Left side panels: single subject fMRI maps showing voxels activated by perforant path stimulation and overlaid on an anatomical T2-weighted image. Right side panels: BOLD time courses averaged (mean SEM) across animals (n=6) and extracted from ipsilateral and contralateral HC and ipsilateral PFC. c, LTP experiment for comparison ((-) AAV infection, (-) CNO administration) showing the expected activation of HC, PFC and NAc in POST-LTP. We note the evoked BOLD responses bilaterally in the HC (right panels), a landmark of HC-response after LTP induction. d, Upper: AAV infection in the NAc ((+) AAV, (-) CNO) preserves activation of the HC under perforant path stimulation before LTP. BOLD signal responses (left panel) are only evident in the ipsilateral HC as expected from PRE-LTP condition. Lower: inactivating the NAc by administration of CNO in the same animal ((+) AAV, (+) CNO) does not alter functional maps nor BOLD responses in the baseline (PRE-LTP) condition. e, NAc inactivation ((+) AAV, (+) CNO) prevents the activation of NAc and PFC induced by LTP (POST-LTP) as predicted by theory.

  The ability to identify essential nodes in the brain has a profound importance in that it helps to understand global information processing. Most importantly, it represents a new paradigm in the identification of brain targets of neuropathological interest and open new therapeutic opportunities oriented to treat network dynamics. Even though we are currently focusing only on memory consolidation in the brain, our theory allows to design intervention protocols for a wide range of tasks due to its generality; interventions are being planned in the near future.

  B. Predicting essential functional areas in the brain with tumor using Collective Influence Theory (NIH-Brain Initiative)

  The identification of core influential nodes essential for proper brain function is applicable to tumor neurosurgery. Typically, neurosurgeons are presented with fMRI activation maps, which depict the locations of eloquent cortices (such as language and motor areas) adjacent to tumors, which neurosurgeons use to plan and guide the resection of gliomas and other intracranial masses. Notwithstanding its advantages, fMRI clearly has limitations. One of the main problems facing the preoperative evaluation of brain tumors by fMRI is that this technology depicts activations of both ’essential’ and ’non-essential’ functional areas. For a neurosurgeon, this distinction is of paramount importance. ’Essential’ language areas are defined as those, whose direct, intraoperative stimulation by electrodes leads to speech arrest. Resection of such an area leads to severe language deficits. In contradistinction, ’non-essential’ language areas are defined as those whose direct stimulation by electrodes does not lead to speech arrest. Resection of such areas is thought to be safe. The current fMRI technology does not allow one to differentiate between these areas. Our Collective Influence method [3] raises the distinct possibility of distinguishing between ’essential’ and ’non-essential’ nodes. By establishing the relative importance of various brain areas following Collective Influence theory, we inform the operating neurosurgeon more precisely of the relative importance of each section of the brain that s/he is planning to resect. Such an advance clearly leads to further improvements in the neurosurgical management of brain tumor patients. The ideas developed in functional brain imaging are tested against the current ’gold standard’ of localizing brain function – direct cortical stimulation of the exposed brain during neurosurgery in collaboration with Dr. Andrei Holodny at the Department of Radiology of Memorial Sloan-Kettering Cancer Center in New York City.

  

  Network of Networks in the Brain

  Neural activity measured in the human brain exhibits weak correlations over long distances. At the same time, activity forms highly correlated and tightly localized clusters, reflecting the functional specialization of different brain areas as described above. A fundamental open question in systems neuroscience is how these local clusters interact at the system scale to generate an integrated whole response without losing local independence, a problem known as the ‘binding problem’. Current paradigms in network theory leave this fundamental question unanswered.

  Small-world and scale-free networks have been proposed to solve this basic conundrum: the brain needs to form modules which ought to be sufficiently independent to guarantee functional specialization and sufficiently connected to bind multiple processors for efficient information transfer. However, the small-world structure presents an intrinsic tension between shortcuts generating small-worlds and the persistence of modularity, a global property unrelated to local clustering as we have shown in our recent studies.

  In a recent study published in PNAS 2012, we present a possible solution to this puzzle. We first show that critical percolation theory unambiguously defines a set of modules made of strong links in functional brain networks. Contrary to the common view, these modules are ‘large-world’ fractal structures and, therefore, are very far from being small-world. This means that information transfer in and out the modules is very inefficient; all distances are too far. However, incorporating the weak ties to the network below a critical percolation threshold converts it into a small-world preserving an underlying backbone of well-defined modules. Remarkably, weak ties are precisely organized as predicted by theory maximizing information transfer with minimal wiring costs. This trade-off architecture is reminiscent of the ‘strength of weak ties’ crucial concept of social networks. Such a design provides a natural solution to the paradox of efficient information flow in the highly modular structure of the brain.

  In a paper published in Nature Physics in Oct 2014 (see cover below) we propose a departure from current models, replacing the concept of small-world by that of hierarchical network of networks (NoN) that describes the brain as a set of hierarchical modules made of strong links interconnected via a sea of weakly correlated links. Our group and collaborators have developed the theory of NoN and applied this new network paradigm to explain network brain activity in resting state and dual-tasking paradigm in humans and rats, see figure. Interestingly, the brain represents a paradigmatic case of a natural NoN and therefore we hypothesize that the NoN theory will capture the functional architecture of brain-wide neuronal networks.  The hypothesis predicts that long-range correlation structure can be drastically altered by affecting link strength and activating or deactivating ‘core’ nodes of the structural network.

  

  References

  1. G. Del Ferraro, A. Moreno, B. Min, F. Morone, U. Pérez-Ramírez, L. Pérez-Cervera, L. C. Parra, A. Holodny, S. Canals, H. A. Makse. Finding essential nodes for integration in the brain using network optimization theory. Nat. Commun. 9, 2274 (2018).

  2. F. Morone, K. Roth, B. Min, H. E. Stanley, H. A. Makse. A model of brain activation predicts the neural collective influence map of the brain. Proc. Nat. Acad. Sci., 114, 3849-3854, (2017).

  3. F. Morone, H. Makse. Influence maximization in complex networks through optimal percolation. Nature 524, 65 (2015).

  4. S. D. S. Reis, Y. Hu, A. Babino, J. S. Andrade Jr., S. Canals, M. Sigman, H. A. Makse. Avoiding catastrophic failure in correlated Networks of Networks. Nat. Phys. 10, 762-767 (2014).

  5. L. K. Gallos, H. A. Makse, M. Sigman. A small world of weak ties provides optimal global integration of self-similar modules in functional brain networks. Proc. Nat. Acad. Sci. 109, 2825-2830 (2012).

  6. L. K. Gallos, H. A. Makse, M. Sigman. The conundrum of functional brain networks: small-world efficiency or fractal modularity. Front. Physiol. 3, 123 (2012).

  7. F. Morone, H. A. Makse, The k-core structural collapse of dynamical complex systems, Nat. Phys., submitted (2016).

  8. M. Kitsak, L. K. Gallos, S. Havlin, F. Liljeros, L. Muchnik, H. Eugene Stanley, H. A. Makse. Identification of influential spreaders in complex networks. Nat. Phys. 6, 888-893 (2010). Cover of November 2010 issue.

  9. C. Song, S. Havlin, H. A. Makse. Self-similarity of complex networks. Nature 433, 392-395 (2005).

  10. C. Song, S. Havlin, H. A. Makse. Origins of fractality in the growth of complex networks. Nat. Phys. 2, 275 (2006).

  11. L. Gallos, C. Song, S. Havlin, H. A. Makse. Scaling theory of transport in biological complex networks. Proc. Nat. Acad. Sci. 104, 7746 (2007).

  12. H. D. Rozenfeld, C. Song and H. A. Makse. The small world-fractal transition in complex networks: a renormalization group approach. Phys. Rev. Lett. 104, 025701 (2010).

  13. V. Galvao, J. G. V. Miranda, R. F. S. Andrade, J. S. Andrade Jr., L. K. Gallos, H. A. Makse. Modularity map of the network of human cell differentiation. Proc. Nat. Acad. Sci. 107, 5750-5755 (2010).

  14. A. Bovet, F. Morone, H. A. Makse, Validation of Twitter opinion trends with national polling aggregates: Hillary Clinton vs Donald Trump, under review Nat. Commun. (2016).

  15. S. Luo, F. Morone, C. Sarraute, H. A. Makse, Inferring personal financial status from social network location, under review Nat. Commun. (2016).

  16. D. Rybski, S. Buldyrev, S. Havlin, F. Liljeros, H. A. Makse. Scaling laws of human interaction activity. Proc. Nat. Acad. Sci. 106, 12640-12645 (2009).

  17. L. K. Gallos, S. Havlin, F. Liljeros, H. A. Makse. How people interact in evolving online affiliation networks. Phys. Rev. X 2, 031014 (2012).

  18. Y. Hu, S. Havlin, H. A. Makse. Conditions for viral influence spreading through correlated multiplex networks. Phys. Rev. X 4, 021031 (2014).

  19. H. A. Makse, S. Havlin, H. E. Stanley. Modelling urban growth patterns. Nature 377, 608-612 (1995).

  20. H. D. Rozenfeld, D. Rybski, J. S. Andrade Jr., M. Batty, H. E. Stanley, H. A. Makse. Laws of population growth. Proc. Nat. Acad. Sci. 105, 18702-18707 (2008).

  21. H. D. Rozenfeld, D. Rybski, X. Gabaix, H. A. Makse. The area and population of cities: New insights from a different perspective on cities. Amer. Econ. Rev. 101, 560-580 (2011).

  22. A. Baule, F. Morone, H. J. Herrmann, H. A. Makse. Edwards statistical mechanics for jammed granular matter. Rev. Mod. Phys., to appear (2017).

  23. A. Baule, R. Mari, L. Bo, L. Portal, H. A. Makse. Mean-field theory of random close packings of axisymmetric particles. Nat. Commun. 4, 2194 (2013).

  24. C. Song, P. Wang, H. A. Makse. Phase diagram of jammed matter. Nature 453, 629-632 (2008).

  25. P. Wang, C. Song, H. A. Makse. Dynamic particle tracking reveals the aging temperature of a colloidal glass. Nat. Phys. 2, 526-531 (2006).

  26. C. Song, P. Wang, H. A. Makse. Experimental measurement of an effective temperature for jammed granular materials. Proc. Nat. Acad. Sci. 102, 2299-2304 (2005).

  27. H. A. Makse, J. Kurchan. Testing the thermodynamic approach to granular matter with a numerical model of a decisive experiment. Nature 415, 614-617 (2002).

  28. H. Makse, S. Havlin, P. King, H. Stanley. Spontaneous stratification in granular mixtures. Nature 386, 379 (1997).

• 

  Superspreaders

  Find the most influential spreaders in online social media.

  Connections are not everything

  ---

  The goal of the science of superspreaders is the identification of the most important nodes in a given network. Indeed, the whole frame of interconnections in complex networks hinges on a specific set of structural nodes, much smaller than the total size, which, (a) if activated in a social network like Twitter, they would cause the spread of information to the whole network; (b) if immunized in a contact network of people, they would prevent the diffusion of a large scale epidemic; and (c) if removed from an infrastructure network like the Internet or power grid, they would cause a cascading collapse of the network. Localizing this optimal, i.e. minimal, set of structural nodes, generically called superspreaders or influencers, in present day big-data networks is one of the most important unsolved problems in contemporary big-data science.

  Thus, the optimal influencer problem applies across a range of important applications in big-data: influential people can be mobilized towards spreading news or consumer products in ‘viral’ marketing campaigns in social media. Superspreaders play a pivotal role in halting epidemics with minimal immunizations, with important applications in epidemiology. Furthermore, protecting these nodes against malicious attacks increases robustness and resilience of many networked systems around us such as the Internet, mobile phone networks, power grids and transportation networks. Finally, in biological information processing networks like the brain, these nodes are responsible for broadcasting the information to the whole system and therefore are the crucial links in the brain network structure.

  Due to these practical implications, there has been an abundant production on the subject of identifying most influential nodes and superspreaders across many disciplines starting from early work in sociology to computer science, mathematics and physics.  The common practice in these fields is the use of heuristic methods based on individual node’s attributes such as the number of connections of a node (the degree) or its PageRank, which is the basis of the Google search algorithm. Even though these heuristic rankings are widely used, they are ambiguous definitions of node’s importance in a network since heuristics do not optimize any objective global function of influence.  As a consequence, there is no guarantee of their performance. Thus, despite the vast use of heuristic strategies to identify influential spreaders, the problem remains unsolved.

  Since 2010 we have been working on this problem.  Originally, we treated the case of identifying single spreaders with k-core percolation. Our study has revealed a surprising feature: “Connections are not everything” for spreading information in social networks but the location of the spreader in the network is more important than its number of friends (Fig. A). The most efficient spreaders are consistently found in the core of the network as identified by k-core percolation, independent of their connectivity.

  The general problem of multiple spreaders that is relevant for brain networks has remained unsolved since it is NP-hard.  As stated above, there is no satisfactory method to answer questions such as how many spreaders are needed for complete network coverage or the extent of coverage as a function of the given number of spreaders, especially for practical applications. Besides these difficulties, in our paper we have recently developed the analytical framework to find the optimal solution to the influencer problem which can predict the minimal number of influencers in complex networks, which, surprisingly, are composed of low-degree (weak) nodes rather than the expected highly-connected nodes or hubs (Fig. B). We have also developed scalable algorithm to approximate the solution in big-data networks. Our approach is supported by rigorous theory using state-of-the-art optimization theory and spin glass theory.

  The data that we used in this study can be downloaded here.

   

  (A)    (B) 

• 

  Complex Networks

  Big-Data Science

  Complex Networks

  The laboratory headed by Prof. Makse at the Levich Institute of City College of New York is devoted to the development of new emergent laws for complex systems ranging from the brain [1, 2, 3], biological networks [4, 5, 6, 7, 8] to social networks [9, 10, 11, 12, 13, 14, 15]. In parallel, we are also interested in the understanding of jamming and structural arrests in soft materials ranging from gran- ular matter, colloids, emulsions and glasses, including spin glasses [16, 17, 18, 19, 20, 21]. We treat these dissimilar systems from a unified theoretical approach using concepts from statistical mechanics of out of equilibrium systems, graph theory, spin-glasses and big-data analytics.

  Our current efforts on Biological Networks are based on the work of our group recently published in Nature (Morone and Makse, 2015) [1] and Nature Physics (Reis et al, 2014) [2] where we described a fundamentally transformative approach to big-data analysis of brain networks and optimization of influence using graph theory.

  We present the first analytical solution to the problem of identification of the most influential nodes (essential nodes) in biological networks [1]; a long-standing problem in big-data science. This problem belongs to the class of non-deterministic polynomial-time hard problems (NP-hard), and therefore it is analogous to the hardest problems in computational science and spin glasses. We have been working on this topic over the last five years since our first publication in November 2010 [9] which has provided evidence that in real-world networks ’connections are not everything’, and has inspired the field of superspreading phenomena in complex networks. Our group has developed a large-scale search engine for localizing the most influential nodes in networks: the Collective Influence (CI) algorithm. CI combines optimality, scalability and versatility, making it applicable to a large class of problems, e.g., from finding influential areas in the brain, to containing epidemic out- break trough targeted immunization interventions, maximizing the spread- ing of information activities for marketing purposes, or quantifying systemic risk in banking systems. Theoretically, Morone and I [1] showed that the influence maximization problem can be exactly mapped to optimal percolation, i.e., finding the minimal set of nodes to destroy the giant connected component of a network into disconnected clusters. We show that tools of combinatorial optimization, spectral theory and spin glasses can be used to find the most influential nodes in the network. We solve the problem by computing the minimal set of nodes that minimizes the largest eigenvalue of the Non-Backtracking (NB) matrix of the network. This operator has recently received a lot of attention thanks to its high performance in the problems of community detection and random percolation in networks, and loop corrections to the Bethe approximation in spin glass models on sparse random graphs. In our study we show the formidable topological power of NB matrices in the problem of Collective Influence in the brain and its consequences for robustness, vulnerability and navigability for networked neural systems. The theory identifies the minimal set of candidate nodes that can lead to cascades of activity in the brain network. The output of the theory provides a ranking of nodes whose inhibition could produce the largest disrupting effect extending to a large portion of the brain. Optimal percolation theory in the brain is one of the main focus of our current research program.

  At some point, we have all agreed that “it’s a small world” to express our surprise over unexpected common acquaintances. This simple phrase has become the symbol of a quiet revolution in our understanding of how complex interactions give rise to simple universal laws. Some decades ago, sociologists determined experimentally that the above expression holds true, but only recently have we been able to understand how it is possible to be within a distance of six handshakes with every person in the world (with an earth population in the billions). More importantly, we have now realized that this proximity is only one of the many counter-intuitive manifestations of a unifying underlying pattern. Such laws are not restricted in social systems only, but seem to cross the borders of many disciplines. See more.

  References

  [1] F. Morone, H. A. Makse. Influence maximization in complex networks through optimal percolation. Nature 524, 65-68 (2015). Accompanied by News & Views Nature editorial by I. A. Kovács, A.-L. Barabási, “Destruction Perfected” (July 2015).

  [2] S. D. S. Reis, Y. Hu, A. Babino, J. S. Andrade Jr., S. Canals, M. Sigman, H. A. Makse. Avoiding catastrophic failure in correlated Networks of Networks. Nature Phys. 10, 762-767 (2014). Accompanied by News & Views Nature Physics editorial “Multilayer Networks: Dangerous Liaisons?” by G. Bianconi (October 2014).

  [3] L. K. Gallos, H. A. Makse, M. Sigman. A small world of weak ties provides optimal global integration of self-similar modules in functional brain networks. Proc. Nat. Acad. Sci. 109, 2825-2830 (2012).

  [4] C. Song, S. Havlin, H. A. Makse. Self-similarity of complex networks. Nature 433, 392-395 (2005).

  [5] C. Song, S. Havlin, H. A. Makse. Origins of fractality in the growth of complex networks. Nature Phys. 2, 275 (2006).

  [6] L. Gallos, C. Song, S. Havlin, H. A. Makse. Scaling theory of transport in biological complex networks. Proc. Nat. Acad. Sci. 104, 7746 (2007).

  [7] H. D. Rozenfeld, C. Song and H. A. Makse. The small world-fractal transition in complex networks: a renormalization group approach. Phys. Rev. Lett. 104, 025701 (2010).

  [8] V. Galvao, J. G. V. Miranda, R. F. S. Andrade, J. S. Andrade Jr., L. K. Gallos, H. A. Makse. Modularity map of the network of human cell differentiation. Proc. Nat. Acad. Sci. 107, 5750-5755 (2010).

  [9] M. Kitsak, L. K. Gallos, S. Havlin, F. Liljeros, L. Muchnik, H. Eugene Stanley, H. A. Makse. Identification of

  influential spreaders in complex networks. Nature Phys. 6, 888-893 (2010). Cover of November 2010 issue.

  [10] D. Rybski, S. Buldyrev, S. Havlin, F. Liljeros, H. A. Makse. Scaling laws of human interaction activity. Proc. Nat. Acad. Sci. 106, 12640-12645 (2009).

  [11] L. K. Gallos, S. Havlin, F. Liljeros, H. A. Makse. How people interact in evolving online affiliation networks. Phys. Rev. X 2, 031014 (2012).

  [12] Y. Hu, S. Havlin, H. A. Makse. Conditions for viral influence spreading through correlated multiplex networks. Phys. Rev. X 4, 021031 (2014).

  [13] H. A. Makse, S. Havlin, H. E. Stanley. Modelling urban growth patterns. Nature 377, 608-612 (1995).

  [14] H. D. Rozenfeld, D. Rybski, J. S. Andrade Jr., M. Batty, H. E. Stanley, H. A. Makse. Laws of population growth. Proc. Nat. Acad. Sci. 105, 18702-18707 (2008).

  [15] H. D. Rozenfeld, D. Rybski, X. Gabaix, H. A. Makse. The Area and Population of Cities: New Insights from a Different Perspective on Cities. American Economic Review 101, 560-580 (2011).

  [16] A. Baule, R. Mari, L. Bo, L. Portal, H. A. Makse. Mean-field theory of random close packings of axisymmetric particles. Nature Comms 4, 2194 (2013).

  [17] C. Song, P. Wang, H. A. Makse. Phase diagram of jammed matter. Nature 453, 629-632 (2008).

  [18] P. Wang, C. Song, H. A. Makse. Dynamic particle tracking reveals the aging temperature of a colloidal glass. Nature Phys. 2, 526-531 (2006).

  [19] C. Song, P. Wang, H. A. Makse. Experimental measurement of an effective temperature for jammed granular materials. Proc. Nat. Acad. Sci. 102, 2299-2304 (2005).

  [20] H. A. Makse, J. Kurchan. Testing the thermodynamic approach to granular matter with a numerical model of a decisive experiment. Nature 415, 614-617 (2002).

  [21] H. A. Makse, S. Havlin, P. R. King, H. E. Stanley. Spontaneous stratification in granular mixtures. Nature 386, 379-381 (1997).

   

• 

  Biological Networks

  Protein Interaction Networks and Genetic Networks

  Biological Network

  ---

  Function and evolution of these networks are among the most fascinating research questions in biology. Bioinformatician Thomas Rattei, University of Vienna, and physicist Hernan Makse, City University New York (CUNY), have reconstructed ancestral protein networks. The results are of high interest not only for evolutionary research but also for the interpretation of genome sequence data. Read more at: Phys.org. Full dataset of reconstructed ancestral protein interaction networks available here.

• 

  Social Networks

  Social Networks

  Social Networks

  ---

  Social scientists have long identified a small number of underlying social mechanisms which individuals follow in the course of interactions with each other. In a recent paper, we performed a multi-scale analysis to investigate how these micro-level social mechanisms of individual actions are transformed into network patterns at the large-scale. We study high-quality data and show how we can estimate the influence of different social drivers underlying evolution of our connections. We developed a systematic study of individual interactions in social communities, with the goal of understanding the process of establishing new network ties.

   

  The frequency of social mechanisms can reveal the global structure of social network as the support for the spreading of infectious diseases. This information can be used to lower the threshold of immunization by identifying those individuals who, through their position in the network, are more likely than average to spread the disease to the larger portion of the social network. In a recent work, we seek a possible way for finding influential spreaders by using the social mechanisms of how social connections are formed in real networks. A reliable immunization scheme can be achieved by surveys such as asking people how they interact with each other. Therefore, not only the effect of network location but also the behavior of individuals is important to design optimal immunization or spreading schemes on social networks.

• 

  Cities

  Predicting urban growth is important for the challenge it presents to theoretical frameworks for cluster dynamics.

  URBAN GROWTH

  ---

  Predicting urban growth is important for the challenge it presents to theoretical frameworks for cluster dynamics. In 1994, the model of diffusion limited aggregation (DLA) has been applied by Mike Batty (CASA) in the book Fractal Cities (Academic Press, 1994) to describe urban growth, and results in tree-like dendritic structures which have a core or “central business district” (CBD). The DLA model predicts that there exists only one large fractal cluster that is almost perfectly screened from incoming “development units” (people, capital, resources, etc), so that almost all the cluster growth occurs in the extreme peripheral tips.

  Our initial work proposed and developed an alternative model to DLA that describes the morphology and the area distribution of systems of cities, as well as the scaling of the urban perimeter of individual cities. Our results agree both qualitatively and quantitatively with actual urban data. The resulting growth morphology can be understood in terms of the effects of interactions among the constituent units forming a urban region, and can be modeled using the correlated percolation model in the presence of a gradient [H. A. Makse, S. Havlin, and H. E. Stanley, Modelling Urban Growth Patterns , Nature 377, 608-612 (1995). Accompanied by News & Views editorial by M. Batty, p. 574. Cover story, “The Shapes of Cities: Mapping out fractal models of urban growth”, Science News 149 , 8-9 (6 Jan 1996); H. A. Makse, J. S. de Andrade, M. Batty, S. Havlin, and H. E. Stanley, Modeling Urban Growth Patterns with Correlated Percolation, Phys. Rev. E (1 December, 1998); H. E. Stanley, L. A. N. Amaral, S. V. Buldyrev, A. L. Goldberger, S. Havlin, H. Leschhorn, P. Maass, H. A. Makse, C.-K. Peng, M. A. Salinger, M. H. R. Stanley, and G. M. Viswanathan, Scaling and Universality in Animate and Inanimate Systems, Physica A 231, 20-48 (1996)].

  Traditional approaches to urban science as exemplified in the work of Christaller, Zipf, Stewart and Warntz, Beckmann, and Krugman are based on the assumption that cities grow homogeneously in a manner that suggests that their morphology can be described using conventional Euclidean geometry. However, recent studies have proposed that the complex spatial phenomena associated with actual urban systems is rather better described using fractal geometry consistent with growth dynamics in disordered media.

  Predicting urban growth dynamics also presents a challenge to theoretical frameworks for cluster dynamics in that different mechanisms clearly drive urban growth from those which have been embodied in existing physical models. In this paper, we develop a mathematical model that relates the physical form of a city and the system within which it exists, to the locational decisions of its population, thus illustrating how paradigms from physical and chemical science can help explain a uniquely different set of natural phenomena – the physical arrangement, configuration, and size distribution of towns and cities. Specifically, we argue that the basic ideas of percolation theory when modified to include the fact that the elements forming clusters are not statistically independent of one another but are correlated, can give rise to morphologies that bear both qualitative and quantitative resemblance to the form of individual cities and systems of cities.

  Comparison between the growth of Berlin and our strongly correlated percolation model:

  Berlin 1875       ………………….. Berlin 1920 ……………….. Berlin 1945

  

   

  Result of the strongly correlated percolation model
  
  We consider the application of statistical physics to urban growth phenomena to be extremely promising, yielding a variety of valuable information concerning the way cities grow and change, and more importantly, the way they might be planned and managed. Such information includes (but is not limited to) the following:
  (i) the size distributions of towns, in terms of their populations and areas;
  (ii) the factal dimensions associated with individual cities and entire systems of cities;
  (iii) interactions or correlations between cities which provide insights into their interdependence;
  (iv) the relevance and effectiveness of local planning policies, particularly those which aim to manage and contain growth.

  The size distribution of cities has been a fundamental question in the theory of urban location since its inception in the late 19th century. In the introduction to his pioneering book published over 60 years ago, Christaller posed a key question: “Are there laws which determine the number, size, and distribution of towns?” This question has not been properly answered since the publication of Christaller’s book, notwithstanding the fact that Christaller’s theory of central places and its elaboration through theories such the rank-size rule for cities embody one of the cornerstones of human geography.

  Our approach produces scaling laws that quantify such distributions. These laws arise naturally from our model, and they are consistent with the observed morphologies of individual cities and systems of cities which can be characterized by a number of fractal dimensions and percolation exponents. In turn, these dimensions are consistent with the density of location around the core of any city, and thus the theory we propose succeeds in tying together both intra- and inter-urban location theories which have developed in parallel over the last 50 years. Furthermore, the striking fact that cities develop a power law distribution without the tuning of any external parameter might be associated with the ability of systems of cities to “self-organize”.

  Map of UK used in our studies of scaling laws of urban centersSo far, we have argued how correlations between occupancy probabilities can account for the irregular morphology of towns in a urban system. The towns surrounding a large city like Berlin are characterized by a wide range of sizes. We are interested in the laws that quantify the town size distribution N(A), where A is the area occupied by a given town or “mass” of the agglomeration, so we calculate the actual distribution of the areas of the urban settlements around Berlin and London, and find that for both cities, N(A) follows a power-law.

  This new result of a power law area distribution of towns, N(A), can be understood in the context of our model. Insight into this distribution can be developed by first noting that the small clusters surrounding the largest cluster are all situated at distances r from the CBD such that p(r) < p_c or

  r > r_f. Therefore, we find N(A), the cumulative area distribution of clusters of area A, to be

  N(A) ~ A^-(tau+1/d_f nu)

  we have plotted the power-law for the area distribution predicted by the above equation along with the real data for Berlin and London. We find that the slopes of the plots for both cities are consistent with the prediction for the case of highly correlated systems. These results quantify the qualitative agreement between the morphology of actual urban areas and the strongly correlated urban systems obtained in our simulations.

  URBAN PLANNING

  Throughout this century, the dominant planning policy in many western nations has been the containment of urban growth. This has been effected using several instruments, particularly through the siting of new settlements or new towns at locations around the growing city which are considered to be beyond commuting distance, but also through the imposition of local controls on urban growth, often coordinated regionally as “green belts”. One of the key elements in the growth models we have proposed here is the characteristic length scale over which growth takes place. In the case of the gradient percolation model, correlations occur over all length scales, and the resulting distributions are fractal, at least up to the percolation threshold.

  In examining the changing development of Berlin in Fig. \ref{dy}a, it appears that the fractal distribution remains quite stable over a period of 70 years and this implies that any controls on growth that there might have been do not show up in terms of the changing settlement pattern, implying that the growth dynamics of the city are not influenced by such control. A rather different test of such policies is provided in the case of London where a green belt policy was first established in the 1930s and rigorously enforced since the 1950s. The question is whether this has been effective in changing the form of the settlement pattern. First, it is not clear that the siting of new towns beyond London’s commuting field was ever beyond the percolation field and thus it is entirely possible that the planned new settlements in the 1950s and 1960s based on existing village and town cores simply reinforced the existing fractal pattern.

  In the same manner, the imposition of local controls on growth in terms of preserving green field land from development seems to have been based on reinforcing the kind of spatial disorder consistent with morphologies generated through correlated percolation. The regional green belt policy was based on policies being defined locally and then aggregated into the green belt itself, and this seems to suggest that the morphology of nondevelopment that resulted was fractal. This is borne out in a fractal analysis of development in the London region which suggests that the policy has little impact on the overall morphology of the area. Moreover, we note that the coincidence between the settlement area distribution for different cities and different years (Berlin 1920 and 1945, and London 1981) suggests that local planning policies such as the green belt may have a relatively low impact on the distribution of towns. Our model suggests that the area distribution is determined by the degree of interactions among development units, and that its scaling properties are independent of time. Current debates on urban growth have now shifted to the development of brownfield sites in cities, and it would be interesting to quantify the extent to which such future developments might reinforce or counter the “natural” growth of the city as implied in these kinds of models.

  To develop more detailed and conclusive insights into the impact of urban policies on growth, it is necessary to develop the model further. This model implies that the area and size distributions, the degree of interaction amongst dependent units of development, and fractal dimension are independent of time. The only time dependent parameter is the gradient lambda and it appears that we might predict future urban forms simply by extrapolating the value of lambda in time. However, we have yet to investigate the influence of topography and other physical constraints on development, the influence of transport routes and the presence of several “independent” central cores or CBDs in the urban region.

  These models can also be further adapted to predict bond as well as site percolation and in future work we will explore the extent to which such interactions between sites and cities might be modeled explicitly. Our interest in such examples is in the universality of the exponents that we have demonstrated here, and which we wish to relate to the impact of urban planning policies.

  More info in the WEB:

  For cities in the world,
  for cities in USA,
  for Swiss cities,
  for Africa population

  • Press release

    Our research has been featured in the press:

    • Nature Editorial by M. Batty, Nature 377, 574 (1995).
    • Science News , Cover story, “The Shapes of Cities: Mapping out fractal models of urban growth”, Science News, 149, 8-9 (6 Jan 1996)
    • Daily Telegraph (London) , Roger Highfield, Sept. 25, 1996.
    • Diario El Pais , Suplemento Futuro, November 1995.
    • Physics World, May 1997, p. 29
    • Scienza & Vita 4, 70 (April 1996).
    • M & P Computer, “La vita artificiale”, A. Vespignani, May 1996, p. 48.
    • Physics World, H. A. Makse, H. E. Stanley, and S. Havlin, ” Power Laws for Cities”, Physics World, 10, 22-23 (October 1997).
    • CSIRO, Division of Wildlife and Ecology.

    Collaborators

    S. Havlin (Bar-Ilan), M. Batty (University College London), J. S. Andrade Jr. (UFC, Brazil), and H. E. Stanley (BU).

  • Picture gallery
    Also available in eps format here.

  North-east of the USA. Population agglomerations identified with the City Clustering Algorithm (CCA) using burning parameter L=1km. The colors from blue to red indicate the number of inhabitants in a logarithmic scale. The Figure covers the Metropolitan Areas Boston, New York, Philadelphia, and Washington.	North-east of the USA. Population agglomerations identified with the City Clustering Algorithm (CCA) using burning parameter L=2km. The colors from blue to red indicate the number of inhabitants in a logarithmic scale. The Figure covers the Metropolitan Areas Boston, New York, Philadelphia, and Washington.
  North-east of the USA. Population agglomerations identified with the City Clustering Algorithm (CCA) using burning parameter L=3km. The colors from blue to red indicate the number of inhabitants in a logarithmic scale. The Figure covers the Metropolitan Areas Boston, New York, Philadelphia, and Washington.	North-east of the USA. Population agglomerations identified with the City Clustering Algorithm (CCA) using burning parameter L=4km. The colors from blue to red indicate the number of inhabitants in a logarithmic scale. The Figure covers the Metropolitan Areas Boston, New York, Philadelphia, and Washington.
  Population clusters for northeastern USA found with the “City Clustering Algorithm” at different length scales, L=1km (upper left), L=2km (upper right), L=4km (lower left), and L=8km (lower right). The smallest clusters, for L=1km, show New York City, Newark, and Jersey City, Boston, Philadelphia, Baltimore, and Washington as separate clusters. As L is increased, small clusters merge. When L=8km, the whole northeastern USA becomes one cluster.	“City Clustering Algorithm” at different length scales, L=1km, L=2km, L=4km, and L=8km (overlapped). The smallest clusters, for L=1km, show New York City, Newark, and Jersey City, Boston, Philadelphia, Baltimore, and Washington as separate clusters. As L is increased, small clusters merge. When L=8km, the whole northeastern USA becomes one cluster.
  CCA applied to the USA.	CCA applied to GB.

• 

  Soft Matter Physics

  Jammed matter studied by conventional and non conventional statistical mechanics.

  Jammed Matter Physics

  ---

  Most recent work: review of Edwards statistical mechanics by Baule, Morone, Herrmann, and Makse, to appear in Rev. Mod. Phys. (2017).

  Random packings of objects of a particular shape are ubiquitous in science and engineering. However, such jammed matter states have eluded any systematic theoretical treatment due to the strong positional and orientational correlations involved. In recent years progress on a fundamental description of jammed matter could be made by starting from a constant volume ensemble in the spirit of conventional statistical mechanics. Recent work has shown that this approach, first introduced by S. F. Edwards more than two decades ago, can be cast into a predictive framework to calculate the packing fractions of both spherical and non-spherical particles. See a Highlight Article in Soft Matter.

  In 1989 Edwards and Oakeshott made the remarkable proposal that the macroscopic properties of static granular matter can be calculated as ensemble averages over equiprobable jammed microstates controlled by the system volume. In other words, granular matter is amenable to a statistical mechanical treatment, where the role of energy is played by the volume. Clearly, there is no a priori reason why such a treatment should be correct. Granular matter is profoundly out of equilibrium, since thermal fluctuations are essentially absent for the macroscopic length scales considered. In particular, there is no equivalent of Liouville’s theorem for equilibrium systems due to the strongly dissipative nature of granular assemblies, which are dominated by static frictional forces. Nevertheless, the Edwards’ ensemble approach has proven exceedingly useful in characterizing the properties of these athermal states of matter and continues to intrigue both experimentalists and theoreticians alike.

  The main assumptions of the Edwards approach are:

  (i) the distribution of jammed microstates is flat and independent of the compaction history leading to a natural definition of a configurational entropy

  S = ln Omega_Edw,

  where Omega_Edw is the number of jammed configurations.

  (ii) There is an equivalence between ensemble averages and time averages, if the system can explore its jammed configurations by some external drive (tapping or slow shearing).

  (iii) The compactivity X =  dS/dV characterizes the packing state analogous to the temperature in equilibrium systems.

  These strong assumptions have been scrutinized in various studies over recent years in order to obtain insight into the validity of Edwards’ approach. Soft compaction experiments under continuous tapping have provided evidence for a reversible branch in the packing fraction for a variation of the tapping amplitude, indicating the existence of thermodynamic states. Simple models of such a compaction dynamics have confirmed ergodicity and have been connected to a slow relaxation dynamics akin to the relaxation in glasses. One signature of such a slow dynamics is the existence of a non-equilibrium fluctuation–dissipation relation. Indeed, the effective temperature appearing in Fluctuation Dissipation Relations under perturbations agrees with the configurational temperature Teff = dS/dE in Edwards’ framework. Ergodicity has also been demonstrated explicitly in more realistic simulations. The compactivity has been measured in simulations and experiments.

  On the other hand, results on the equiprobability of microstates are mixed. By evaluating the probabilities of jammed microstates in small clusters a break down of the flat distribution assumption has been demonstrated, which might be traced back to the packing protocol used. Recent studies have investigated the equilibration of granular subsystems in contact, providing further insight into the thermodynamic nature of granular matter. Ultimately, the success of any statistical mechanical theory needs to be measured by the comparison with experiments.

  One key problem in Edwards’ approach is to identify a suitable volume function, which parametrizes the total volume of the packing as a function of the particle configurations (positions and orientations), replacing the role of the Hamiltonian. Here, different conventions can be employed to partition the total volume into cells associated with each particle, the simplest of which is the Voronoi tessellation. In 3D these exact volume functions are difficult to handle analytically, so that reduced representations are sought. The thermodynamic nature of packings suggests to use a coarse-grained description of the volume function in terms of observables such as the average number of contacts z (coordination number). In turn, z is determined by the force transmission in the contact network leading to a mechanically stable packing in which forces and torques on each particle balance. For the force network ensemble approaches similar to the volume ensembles have been introduced in order to explain the observed force distribution from an entropy maximization. The stress tensor has also been considered as a conserved quantity leading to a different class of ensembles.

  Recently, the force transmission has been treated on a random graph under local mechanical stability constraints resulting in quantitative predictions for the force distribution and the value of z using a cavity method. The problem of finding the densest random packing can be similarly formulated as a constraint optimization problem: random close packings appear as the ground state of the volume ensemble restricted to disordered packings as X tends to 0 for a given z.  This picture highlights that jamming falls into the class of NP constraint optimization problems, which can be tackled successfully with the methods of statistical mechanics such as cavity methods. A full solution needs to combine the two approaches for the force and volume ensembles, where the Hamiltonian that enforces jamming is a function of both the particle configurations and the contact forces on a random contact network. These ensemble approaches are thus similar in spirit to other recent works that consider jamming as the infinite pressure limit of metastable glass phases. Here, one considers instead of the Edwards entropy S, the “glass complexity” in order to obtain the statistics of the metastable basins as the pressure diverges. Treatments of this problem based on the random-first order transition picture and replica theory have been performed.

  Our main results could be condensed into a phase diagram for jammed packings which includes: spherical particles and non-spherical, frictional and frictionless packings, adhesive forces and electrostratic forces as shown below:

  

  We optimize packings in the space of particles shapes by developing a unifying way to generate different particles based on union and intersection of spheres. From dimers, to trimers, to ellipsoids and tetrahedra, a unifying theory can be constructed from Edwards ensemble to predict the density, rigidity and dissipative properties of random packings in terms of the shape of the constitutive particles:

  

  Structural Properties of Random Packings

  A recent paper by Kyeyune-Nyombi, Morone, Liu, Li, Gilchrist, and Makse explores a new method for high-resolution determination of the contact networks of random packings using fluorophore signal exclusion.

  One major difficulty in the investigation of jammed colloidal systems is looking inside of a packing. Experimental tests of theoretical predictions about particulate packings depend upon knowing exactly the contact networks of the packings; this requires a high enough resolution that we can know even fragile contacts at the marginal stability state during the jamming transition. Current methods are effective for analysis of larger grains but do not provide high enough resolution on smaller colloidal length scales.

  The new method outlined in this paper involves the use of quantum dot fluorophore signal exclusion to find inter-particle contacts in packings of colloidal particles, which are important for testing theoretical predictions of (for example) force distribution or stability of packings close to the marginally stable state. The fluorescence, and not the size, of quantum dots is measured, allowing for the possibility that resolution could be even further enhanced using smaller probes.

  The following video shows the structure of part of a packing. Inter-particle contacts can be clearly seen with the help of the new fluorophore exclusion technique. The green rings are the outside edges of quantum dot nanoparticles in solution, which are fluorescent due to AlexaFluor® 488 on their surfaces; the red image shows the same particles but now with red fluorescence.